The blend files can be found here: blendfiles

Paperwork
This post is a high level overview and avoids most of the math details. For anyone interested in the theory here are some useful papers and links:
- Matthias Müller is one of the authors of the PBD and XPBD papers. His video series on softbody simulations is a great introduction: 10 Minute Physics on Youtube
- Müller, Matthias, et al. “Position based dynamics.”
- Macklin, Miles, Matthias Müller, and Nuttapong Chentanez. “XPBD: position-based simulation of compliant constrained dynamics.”
- Müller, Matthias, et al. “Detailed rigid body simulation with extended position based dynamics.”
Position-based dynamics
Position-based Dynamics (PBD) is a technique in softbody simulations for games and movies. It has some advantages over older velocity-based techniques, which the current Blender cloth simulation uses.
While both methods have pros and cons, PBD has become the de facto standard where speed is more important than accuracy, with velocity constraints only being used where they are a natural choice (e.g. friction).
Stages
The node tree is organized into groups that largely match the steps described in (X)PBD papers.
Initializing attributes
The first thing to do is to initialize some attributes for physical properties.
mass: Each vertex represents a section of the cloth and needs a non-zero mass value. For this test it can arbitrarily be set to 1, it doesn’t have to be a realistic value.velocity: Part of the state in any physics sim. For now we just start at rest (v==0).
Setting up Constraints
Constraints for the edge length can be computed in advance. The rest length does not change over time and all the edges take part in the simulation, so we don’t have to recompute anything in later frames. If features like cloth tearing were added the edge constraints may require a partial update later. Collision and pinning constraints are updated at the beginning of each simulation step because they are expected to change as the cloth moves, or gets picked up and dropped.
Collision contacts makes use of the Geometry Proximity and Sample Nearest Surface nodes (previously Transfer Attribute). Contacts that are too far away are ignored. What is “too far”? A point is allowed to travel a certain distance in one step (has a maximum velocity). This helps us limit the potential range of contacts we need to check each frame. We only store one contact per vertex here, a production feature should keep multiple potential contacts to handle more complex collisions.
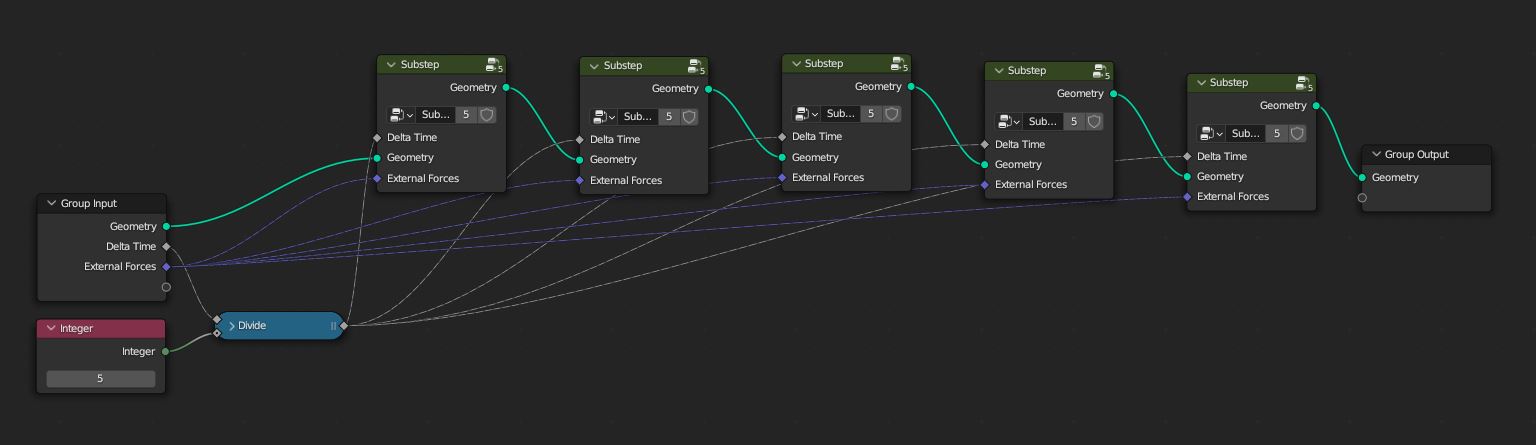
Substeps
Keeping the travel distance per step limited helps with collision handling. This requires that the animation frame is split into multiple simulation sub-steps. Matthias Müller has a good explanation of the issue in cloth simulation: https://www.youtube.com/watch?v=XY3dLpgOk4Q&t=42s
Another reason we want to use substepping is that the Jacobi solver does not converge very fast and large time steps can lead to rubbery cloth behavior. See Solving positional constraints.
Since we don’t have general loop nodes yet i just picked an arbitrary fixed number of 5 substeps, which works reasonably well for this demo.
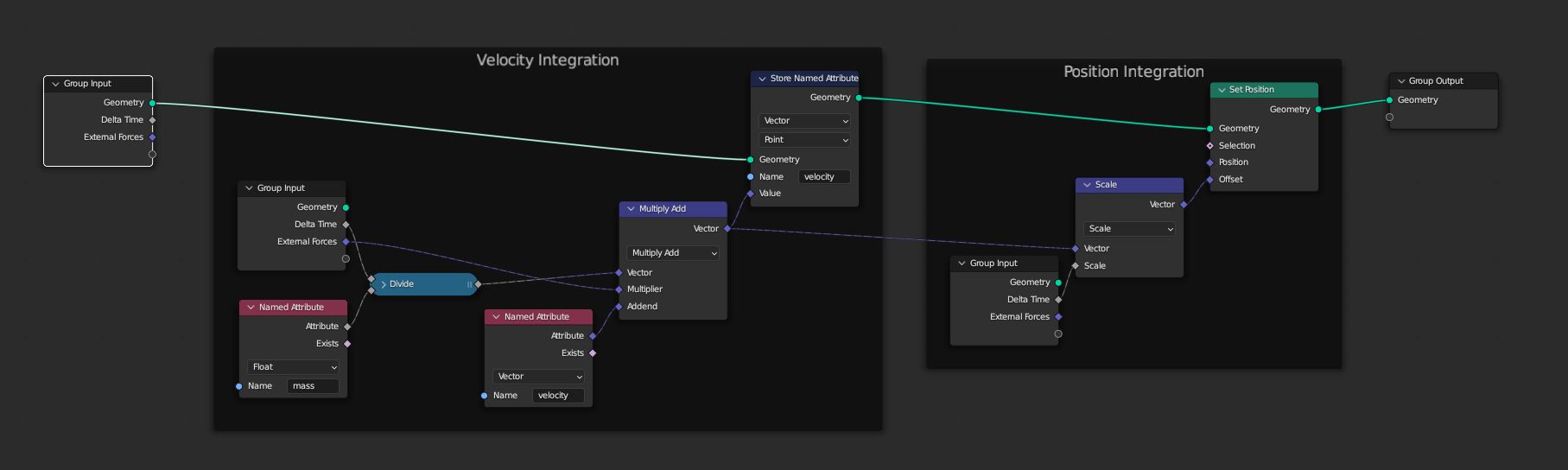
Newtonian motion
Before we try to solve constraints, we first need to compute the unconstrained movement of the vertices. This is done with a symplectic integration, meaning the velocity is integrated first, followed by a position update.
This node also applies any external forces that might be acting on the simulation, such as gravity, wind, and other force fields.
Solving positional constraints
Constraints in a physics simulation are generally applied using the method of Lagrange Multipliers. Intuitively this means moving points in the “best” direction to reduce the constraint distance. For example:
- To solve an edge-length constraint the point is moved along the edge until the length matches the rest length.
- To avoid collision a point is moved along the surface normal until it is outside the collider.
- For a pinning constraint the point is moved towards the pinned point.
The Jacobi method is used in this experiment because it is the easiest to implement in geometry nodes at the current time. The constraint solver is repeated an arbitrary number of times to improve the solution.
For a more detailed description of constraint solvers see Solver methods.
Velocity update
After the positions have been corrected to satisfy constraints we need to recalculate velocities. As a justification consider a ball that collides with a table. After the collision constraint is solved the ball sits on the table without moving. If it’s velocity state is unchanged, however, it will keep getting “faster” due to gravity and each frame a larger positional error has to be corrected.
The velocity is recomputed with a simple finite difference method.
Solving friction constraints
Frictional constraints are special because they apply directly to the velocity instead of the position. The approach used in this demo is described in Müller, Matthias, et al. “Detailed rigid body simulation with extended position based dynamics”. For each contact point the tangential velocity defines the constraint gradient direction.
Solver methods
While solving a single constraint on its own is simple, we usually have to solve multiple constraints together that might push and pull vertices in different directions. There are a number of different methods for solving such systems:
-
Sparse matrix solvers (aka “global” solvers) are accurate and can solve linear systems in a single iteration. However, implementing a sparse matrix solver with just geometry nodes is not really feasible at this point.

Matrix solvers also require that all equations be linear, which can be a problem with the often non-linear physics equations. An interesting option here is Projective Dynamics, e.g. the paper by Bouaziz et al.: “Fusing constraint projections for fast simulations”. This is a topic for another day …
-
Gauss-Seidel solvers are the suggested method in (X)PBD. They solve each constraint on its own (“local” solver), then iterate over the whole set of constraints multiple times. The resulting solution may violate all but the last-solved constraints, but it converges quickly over a few iterations. We can chose to solve the most important constraints last so they are solved perfectly at the end of a time step (e.g. handle collisions last).

The problem with GS solvers is that they require solving constraints in sequence, and loops are not available in geometry nodes yet. One improvement, originally developed for GPU implementations, is to sort vertices into independent subsets using a graph-coloring algorithm. This would enable a GS solver in geometry nodes with a limited number of steps, but graph coloring itself needs to be implemented first.
-
Jacobi’s method is similar to the Gauss-Seidel method, it also solves constraints separately. Instead of applying solutions on top of each other, however, the Jacobi method averages out the solutions. It converges much slower than the Gauss-Seidel method, but has the advantage that it can be easily parallelized, which lends itself to geometry nodes.

It’s still quite complicated to average the solution vectors over all edges of a vertex though. First a utility geometry with 2 points per edge is created. A solution to edge length is calculated for both points of each edge. Then the Accumulate Field node is used to sum up all solutions for a particular vertex and average them. Finally by using the vertex index as a coordinate we can transfer the solution from any of the utility points back to the original vertices.
Conclusion
This was a fun little exercise and i’m very happy that it worked at all. Some of the improvements i’d like to see in the future:
- General loop support: The main concern here is that it inadvertently freeze Blender if loops get too long.
- For a Gauss-Seidel solver it would certainly make sense to implement graph coloring first in order to make best use of multithreading.
- Easier convolution methods would be useful, like averaging over all edges of a vertex.
- Better collision detection algorithms are going to be needed for physics sims in the future (e.g. GJK, convex decomposition)
Simulation nodes offer exciting new possibilities and i hope to explore more areas in the future, like hair and rigid body simulation. I hope this article helps explain some of the concepts in physics simulations and how they might be implemented in node-based form in Blender.
]]>